문인철 교수님의 ‘데이터 구조 및 분석: Linear Structure and Dynamic Programming’ 수업

Big-Oh Notation

Big-O는 알고리즘의 효율성을 나타내는 지표입니다. Big-O를 이용하여 내가 개선한 알고리즘이 빨라졌는지, 메모리를 많이 잡아 먹지는 않는지 등의 알고리즘의 성능을 판단합니다.
Big-O는 대부분 최악의 경우를 표현한다

시간복잡도

시간 복잡도란 big-O에 대한 시간 개념으로 알고리즘의 수행 시간이 얼마인지를 나타냅니다. 수행되는 연산의 수를 가지고 계산하며 알고리즘에서 중요하지 않는 값들은 최대한 무시합니다.
O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(2ⁿ) < O(n!) < O(nⁿ)
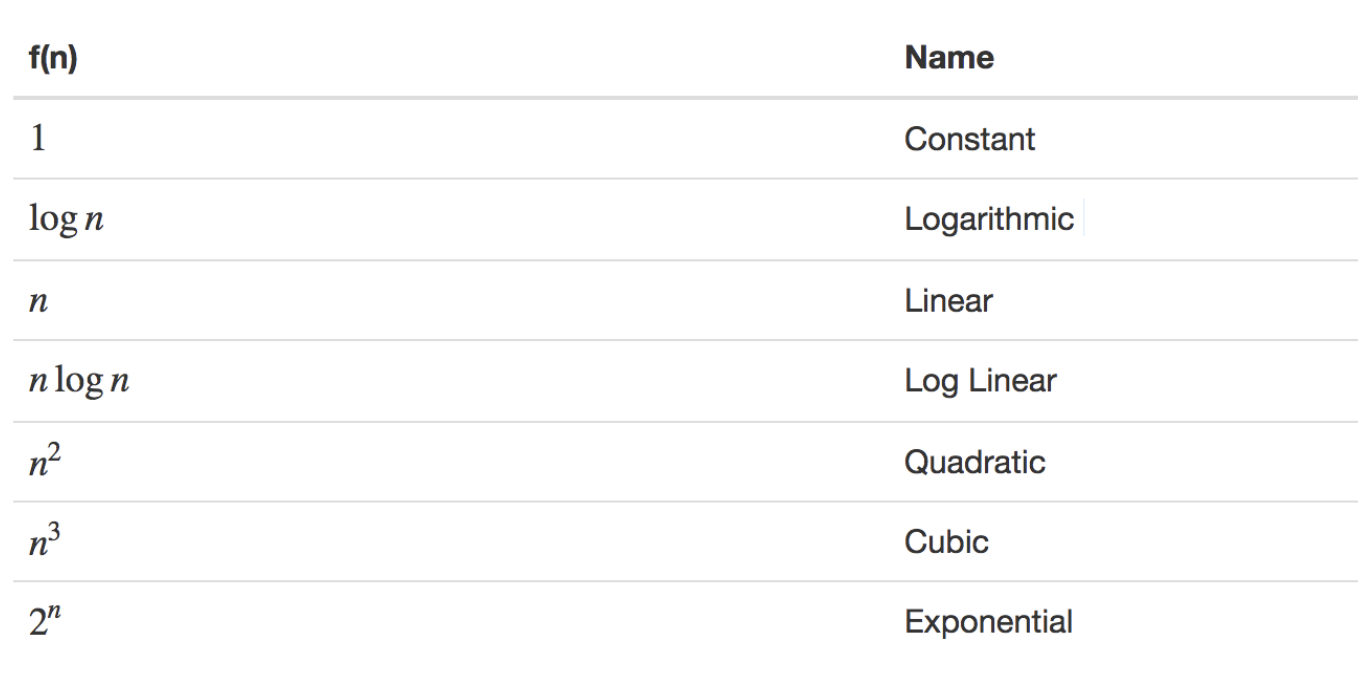
O(1) - (상수) Constant - 입력되는 데이터양과 상관없이 일정한 실행 시간 - 알고리즘이 문제를 해결하는데 오직 한 단계만
O(logN) Logarithmic - 데이터양이 많아져도, 시간이 조금씩 늘어난다. - 시간에 비례하여, 탐색 가능한 데이터양이 2의 n승이 된다. - 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어든다. - 만약 입력 자료의 수에 따라 실행 시간이 이 log N 의 관계를 만족한다면 N이 증가함에 따라 실행시간이 조금씩 늘어난다. 이 유형은 주로 커다란 문제를 일정한 크기를 갖는 작은 문제로 쪼갤때 나타나는 유형이다. - Binary Search
O(N) Linear - 데이터양에 따라 시간이 정비례한다. - linear search, for 문을 통한 탐색을 생각하면 되겠다.
O(N log N) log linear - 데이터양이 N배 많이 진다면, 실행 시간은 N배 보다 조금더 많아 진다. (정비례 하지 않는다.) - 이 유형은 커다란 문제를 독립적인 작은 문제로 쪼개어 각각에 대해 독립적으로 해결하고,나중에 다시 그것들을 하나로 모으는 경우에 나타난다. N이 두배로 늘어나면 실행 시간은 2배보다 약간 더 많이 늘어난다. - 퀵소트, 머지소트
O(N^2) Quadratic - 데이터양에 따라 걸리는 시간은 제곱에 비례한다. (효율이 좋지 않음, 사용하면 안된다) - 이 유형은 이중루프내에서 입력 자료를 처리 하는 경우에 나타난다. N값이 큰값이 되면 실행 시간은 감당하지 못할 정도로 커지게 된다. - 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱 - 2중 for 문을 사용하는 버블소트, 삽입정렬(insertion sort)

공간복잡도

공간에 대한 개념으로 알고리즘이 공간을 얼마나 필요로 하는지를 나타냅니다. 시간 복잡도 보다는 덜 중요시 취급되지만 신경 써봐야 할 필요가 있습니다.예를 들어, 크기가 N인 배열을 만든다고 가정하면 공간 복잡도가 O(N)이 되고 NxN인 배열을 만들면 O(N²)이 됩니다.
함수의 재귀적인 호출의 경우 스택 공간도 고려해야 합니다.