문인철 교수님의 ‘데이터 구조 및 분석: Linear Structure and Dynamic Programming’ 수업
Tree Traversing
다양한 방법으로 트리 데이터를 프린트 할 수 있음
- The value in LHS
- The value is RHS
- The value that you have
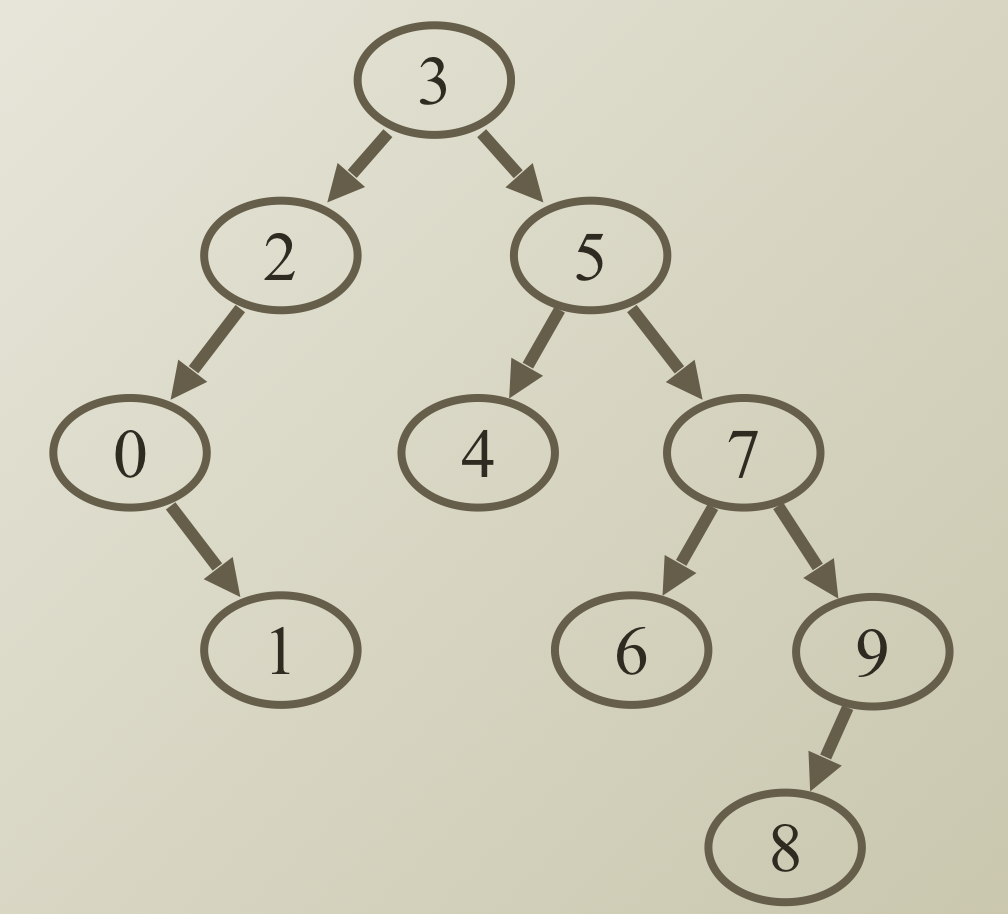
Depth first traverse
 Untitled.png)
Untitled.png)
Pre-order traverse
- 순서: Current, LHS, RHS
- ex) 3, 2, 0, 1, 5, 4, 6, 9, 8
In-order traverse
- 순서: LHS, Current, Rhs
- ex) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Post-order traverse
- 순서: LHS, RHS, Current
- ex) 1, 0, 2, 4, 6, 8, 9, 7, 5, 3
코드
def traverse_in_order(self, node = None):
# LHS -> Current -> RHS
if node is None:
node = self.root
ret = list()
if node.get_lhs() is not None:
ret = ret + self.traverse_in_order(node.get_lhs())
ret.append(node.get_value())
if node.get_rhs() is not None:
ret = ret + self.traverse_in_order(node.get_rhs())
return ret
def traverse_pre_order(self, node = None):
# Current -> LHS -> RHS
if node is None:
node = self.root
ret = list()
ret.append(node.get_value())
if node.get_lhs() is not None:
ret = ret + self.traverse_pre_order(node.get_lhs())
if node.get_rhs() is not None:
ret = ret + self.traverse_pre_order(node.get_rhs())
return ret
def traverse_post_order(self, node = None):
# RHS -> LHS -> Current
if node is None:
node = self.root
ret = list()
if node.get_lhs() is not None:
ret = ret + self.traverse_post_order(node.get_lhs())
if node.get_rhs() is not None:
ret = ret + self.traverse_post_order(node.get_rhs())
ret.append(node.get_value())
return ret
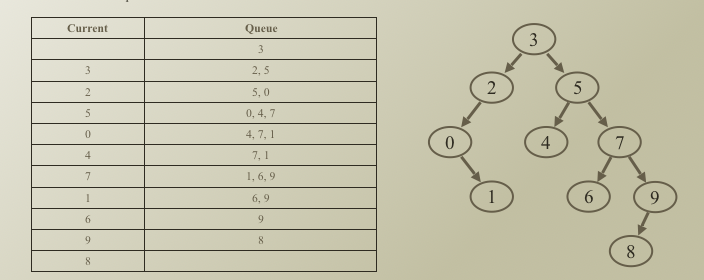
Breadth first traverse
 Untitled.png)
Untitled.png)
- Queue-based level-order traverse - ex) 3, 2, 5, 0, 4, 7, 1, 6, 9, 8
- Enqueue the root - queue 가 비어있을 때까지 - Current = Dequeue one element - LHS가 있으면, Enqueue LHS - RHS가 있으면, Enqueue RHS
코드
class Node:
next_node = None
prev_node = ''
value = ''
is_head = False
is_tail = False
def __init__(self, value = '', next_node = None,
is_head = False, is_tail = False):
self.next_node = next_node
self.value = value
self.is_head = is_head
self.is_tail = is_tail
def get_value(self):
return self.value
def set_value(self, value):
self.value = value
def get_next(self):
return self.next_node
def set_next(self, next_node):
self.next_node = next_node
def is_head(self):
return self.is_head
def is_tail(self):
return self.is_tail
class SinglyLinkedList:
node_head = ''
node_tail = ''
size = 0
def __init__(self):
self.node_tail = Node(is_tail=True)
self.node_head = Node(is_head=True, next_node=self.node_tail)
def insert_node(self, value, index):
new_node = Node(value = value)
prev_node = self.get(index - 1)
next_node = prev_node.get_next()
prev_node.set_next(new_node)
new_node.set_next(next_node)
self.size += 1
def remove_node(self, index_to_remove):
prev_node = self.get(index_to_remove - 1)
node_to_remove = prev_node.get_next()
next_node = node_to_remove.get_next()
prev_node.set_next(next_node)
self.size -= 1
def get(self, index):
result_node = self.node_head
for i in range(index + 1):
result_node = result_node.get_next()
return result_node
def get_size(self):
return self.size
def print_status(self):
current_node = self.node_head
while current_node.get_next().is_tail == False:
current_node = current_node.get_next()
print(f'{current_node.get_value()} > ', end = "")
class Queue:
linked_list = SinglyLinkedList()
def dequeue(self):
# 이전 코드의 경우, dequeue 를 하면서 노드를 삭제했기때문에
# tree_node 를 리턴하고 삭제되도록 수정
tree_node = self.linked_list.get(0).value
self.linked_list.remove_node(0)
return tree_node
def enqueue(self, value):
self.linked_list.insert_node(value, self.linked_list.get_size())
def is_empty(self):
return self.linked_list.get_size() == 0
class BinarySearchTree:
root = None
'''이전 코드 생략'''
def traverse_leval_order(self):
ret = []
queue = Queue()
queue.enqueue(self.root)
while not queue.is_empty():
node = queue.dequeue()
if node is None:
continue
ret.append(node.get_value())
if node.get_lhs() is not None:
queue.enqueue(node.get_lhs())
if node.get_rhs() is not None:
queue.enqueue(node.get_rhs())
return ret
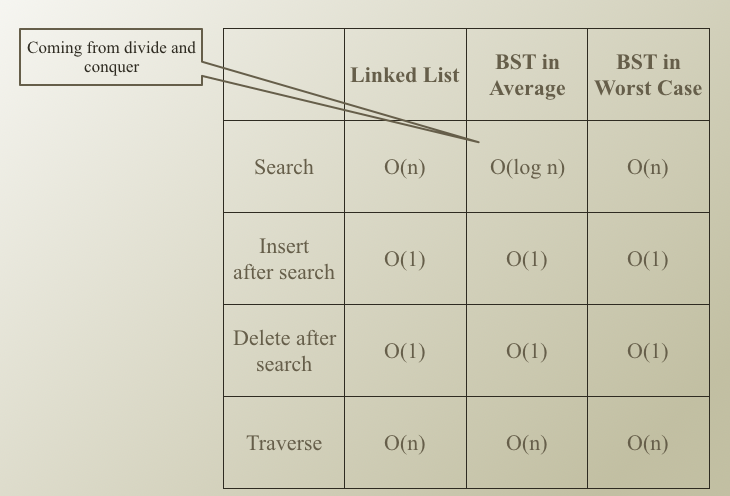
Performance of binary search tree
- average case 의 경우 height 에 따라서 성능이 달라진다.
 Untitled.png)
Untitled.png)
Binary Search Tree code
class Node:
next_node = None
prev_node = ''
value = ''
is_head = False
is_tail = False
def __init__(self, value = '', next_node = None,
is_head = False, is_tail = False):
self.next_node = next_node
self.value = value
self.is_head = is_head
self.is_tail = is_tail
def get_value(self):
return self.value
def set_value(self, value):
self.value = value
def get_next(self):
return self.next_node
def set_next(self, next_node):
self.next_node = next_node
def is_head(self):
return self.is_head
def is_tail(self):
return self.is_tail
class SinglyLinkedList:
node_head = ''
node_tail = ''
size = 0
def __init__(self):
self.node_tail = Node(is_tail=True)
self.node_head = Node(is_head=True, next_node=self.node_tail)
def insert_node(self, value, index):
new_node = Node(value = value)
prev_node = self.get(index - 1)
next_node = prev_node.get_next()
prev_node.set_next(new_node)
new_node.set_next(next_node)
self.size += 1
def remove_node(self, index_to_remove):
prev_node = self.get(index_to_remove - 1)
node_to_remove = prev_node.get_next()
next_node = node_to_remove.get_next()
prev_node.set_next(next_node)
self.size -= 1
def get(self, index):
result_node = self.node_head
for i in range(index + 1):
result_node = result_node.get_next()
return result_node
def get_size(self):
return self.size
def print_status(self):
current_node = self.node_head
while current_node.get_next().is_tail == False:
current_node = current_node.get_next()
print(f'{current_node.get_value()} > ', end = "")
class Queue:
linked_list = SinglyLinkedList()
def dequeue(self):
# 이전 코드의 경우, dequeue 를 하면서 노드를 삭제했기때문에
# tree_node 를 리턴하고 삭제되도록 수정
tree_node = self.linked_list.get(0).value
self.linked_list.remove_node(0)
return tree_node
def enqueue(self, value):
self.linked_list.insert_node(value, self.linked_list.get_size())
def is_empty(self):
return self.linked_list.get_size() == 0
class TreeNode:
lhs_node = None
rhs_node = None
parent_node = None
value = None
def __init__(self, value, parent_node):
self.value = value
self.parent_node = parent_node
def get_lhs(self):
return self.lhs_node
def get_rhs(self):
return self.rhs_node
def get_value(self):
return self.value
def get_parent(self):
return self.parent_node
def set_lhs(self, lhs_node):
self.lhs_node = lhs_node
def set_rhs(self, rhs_node):
self.rhs_node = rhs_node
def set_value(self, value):
self.value = value
def set_parent(self, parent_node):
self.parent_node = parent_node
class BinarySearchTree:
root = None
def __init__(self):
pass
def insert(self, value, node = None):
# escape
if node is None:
# node 가 없는 경우 root 로 지정
node = self.root
if self.root is None:
# 가장 처음 insert 하는 경우
self.root = TreeNode(value, None)
return
if value == node.get_value():
# 이미 value 가 존재하는 경우
return
# recursion
if value > node.get_value():
if node.get_rhs() is None:
new_node = TreeNode(value, node)
node.set_rhs(new_node)
else:
self.insert(value, node.get_rhs())
if value < node.get_value():
if node.get_lhs() is None:
new_node = TreeNode(value, node)
node.set_lhs(new_node)
else:
self.insert(value, node.get_lhs())
return
def search(self, value, node = None):
if node is None:
node = self.root
if value == node.get_value():
return True
if value > node.get_value():
if node.get_rhs() is None:
return False
else:
return self.search(value, node.get_rhs())
if value < node.get_value():
if node.get_lhs() is None:
return False
else:
return self.search(value, node.get_lhs())
def delete(self, value, node = None):
if node is None:
node = self.root
if node.get_value() < value:
return self.delete(value, node.get_rhs())
if node.get_value() > value:
return self.delete(value, node.get_lhs())
if node.get_value() == value:
# two child
if (node.get_lhs() is not None
and node.get_rhs() is not None):
min_node = self.find_min_value(node.get_rhs())
node.set_value(min_node.get_value())
self.delete(min_node.get_value(), node.get_rhs())
return
parent = node.get_parent()
# one child
if node.get_lhs() is not None:
if node == self.root:
self.root = node.get_lhs()
elif parent.get_lhs() == node:
parent.set_lhs(node.get_lhs())
node.get_lhs().set_parent(parent)
else:
parent.set_rhs(node.get_lhs())
node.get_lhs().set_parent(parent)
return
if node.get_rhs() is not None:
if node == self.root:
self.root = node.get_rhs()
elif parent.get_lhs() == node:
parent.set_lhs(node.get_rhs())
node.get_rhs().set_parent(parent)
else:
parent.set_rhs(node.get_rhs())
node.get_rhs().set_parent(parent)
return
# no child
if node == self.root:
self.root = None
elif parent.get_lhs == node:
parent.set_lhs(None)
else:
parent.set_rhs(None)
return
def find_max_value(self, node = None):
if node is None:
node = self.root
if node.get_rhs() is None:
return node.value
return self.find_max_value(node.get_rhs())
def find_min_value(self, node = None):
if node is None:
node = self.root
if node.get_lhs() is None:
return node.value
return self.find_min_value(node.get_lhs())
def traverse_leval_order(self):
ret = []
queue = Queue()
queue.enqueue(self.root)
while not queue.is_empty():
node = queue.dequeue()
if node is None:
continue
ret.append(node.get_value())
if node.get_lhs() is not None:
queue.enqueue(node.get_lhs())
if node.get_rhs() is not None:
queue.enqueue(node.get_rhs())
return ret
def traverse_in_order(self, node = None):
# LHS -> Current -> RHS
if node is None:
node = self.root
ret = list()
if node.get_lhs() is not None:
ret = ret + self.traverse_in_order(node.get_lhs())
ret.append(node.get_value())
if node.get_rhs() is not None:
ret = ret + self.traverse_in_order(node.get_rhs())
return ret
def traverse_pre_order(self, node = None):
# Current -> LHS -> RHS
if node is None:
node = self.root
ret = list()
ret.append(node.get_value())
if node.get_lhs() is not None:
ret = ret + self.traverse_pre_order(node.get_lhs())
if node.get_rhs() is not None:
ret = ret + self.traverse_pre_order(node.get_rhs())
return ret
def traverse_post_order(self, node = None):
# RHS -> LHS -> Current
if node is None:
node = self.root
ret = list()
if node.get_lhs() is not None:
ret = ret + self.traverse_post_order(node.get_lhs())
if node.get_rhs() is not None:
ret = ret + self.traverse_post_order(node.get_rhs())
ret.append(node.get_value())
return ret