문인철 교수님의 ‘데이터 구조 및 분석: Linear Structure and Dynamic Programming’ 수업

Insert and Search Operation of Binary Search Tree

Insert operation of binary search tree

추가하려는 value 가 이미 존재하는 경우
- 중복하지 않기 위해서 해당 노드에서 return
추가하려는 value 가 현재 위치의 노드보다 경우
- right-hand-side 에 노드가 있으면 RHS 노드 쪽으로 이동 (Recursion)
- right-hand-side 노드가 없는 경우 추가하려는 Value 를 insert
추가하려는 value 가 현재 위치의 노드보다 작은 경우
- left-hand-size 노드가 있으면 LHS 노드 쪽으로 이동 (Recursion)
- left-hand-size 노드가 없는 경우 추가하려는 value 를 insert

코드

def insert(self, value, node = None):
        # escape          
        if node is None:
            # node 가 없는 경우 root 로 지정    
            node = self.root
        if self.root is None:
            # 가장 처음 insert 하는 경우 
            self.root = TreeNode(value, None)
            return 
        if value == node.get_value():
            # 이미 value 가 존재하는 경우  
            return 
        
        # recursion         
        if value > node.get_value():
            if node.get_rhs() is None:
                new_node = TreeNode(value, node)
                node.set_rhs(new_node)
            else:              
                self.insert(value, node.get_rhs())
        if value < node.get_value():
            if node.get_lhs() is None:
                new_node = TreeNode(value, node)
                node.set_lhs(new_node)
            else:
                self.insert(value, node.get_lhs())
        return

Search operation of binary search tree

찾는 value 를 찾는 경우 - return True
찾는 value 가 현재 노드 value 값 보다 큰 경우 - RHS 노드가 있는 경우 RHS 노드쪽으로 이동 (Recursion) - RHS 노드가 없는 경우 return False (찾는 값이 없음)
찾는 value 가 현재 노드 value 값 보다 작은 경우 - LHS 노드가 있는 경우 LHS 노드쪽으로 이동 (Recursion) - LHS 노드가 없는 경우 return False (찾는 값이 없음

그림예시

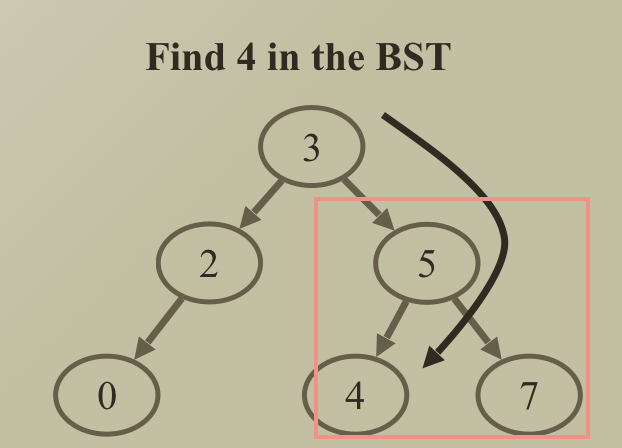
4 를 찾는 경우 root 보다 큰 값이기 때문에 RHS 쪽만 찾으면 됨
linked list 경우엔 모든 노드를 다 찾아봐야한다 → O(N)

코드

def search(self, value, node = None):
        if node is None:
            node = self.root
        if value == node.get_value():
            return True
        if value > node.get_value():
            if node.get_rhs() is None:
                return False
            else:
                return self.search(value, node.get_rhs())
        if value < node.get_value():
            if node.get_lhs() is None:
                return False
            else:
                return self.search(value, node.get_lhs())