문인철 교수님의 ‘데이터 구조 및 분석: Linear Structure and Dynamic Programming’ 수업

Dynamic Programming

하위 인스턴스가 반복되서 정의되거나, 반복되는 문제를 해결하기 위해 사용되는 알고리즘
부분 문제 반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간 내에 풀 때 사용
동적 계획법은 부분 문제를 통해 큰 문제를 재귀적으로 해결하려고 할 때 중복되는 부분 문제들이 많이 발생하여 불필요하게 같은 계산이 반복될 때 사용된다.

기본 개념

큰 단위의 문제를 더 작은 인스턴스로 나눈다
작은 인스턴스를 해결
해당 해결 결과를 table 에 저장
테이블에서 큰 인스턴스의 솔루션을 구함

Memoization

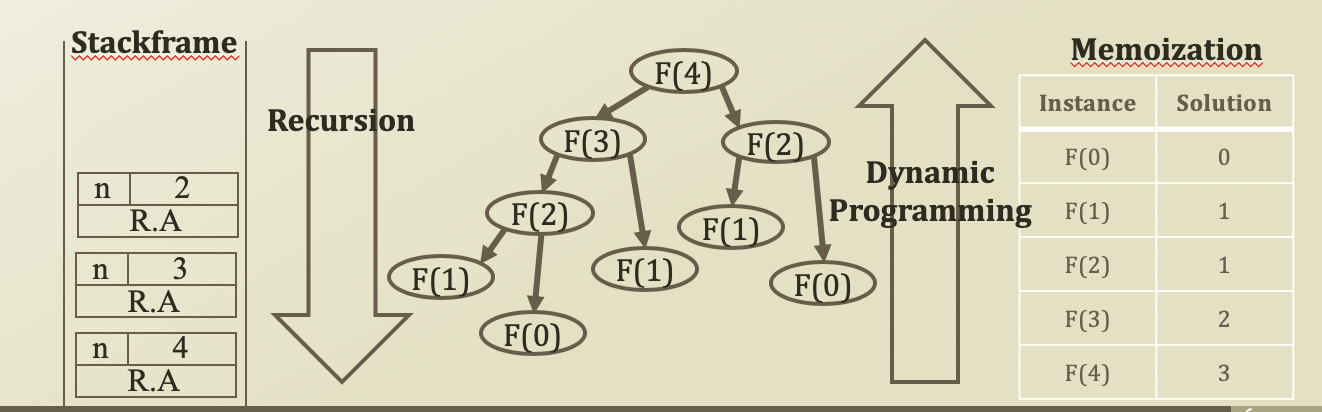
dyanmic programmin 주요 기술
simply put: 이전 함수 호출 결과를 저장하여 나중에 결과를 다시 재사용
more philosophical sense - 문제해결을 위해 상향식 접근 방법(Bottom - up) - 재귀: Top-down - 동적: Bottom-up

Fibonacci Sequence in DP

    # Fibonacci Sequence in DP
    def fibonacci_dp(n):
        # setting up memoization table 
        dic_fibonacii = {
            0: 0,
            1: 1,
        }
        # building up a bigger solutions
        if n >= 2:
            for i in range(2, n + 1):
                dic_fibonacii[i] = dic_fibonacii[i - 1] + dic_fibonacii[i - 2]
        
        return dic_fibonacii[n]
    
    for i in range(0, 10):
        print(fibonacci_dp(i))

결론

memoization table O(N) 개까지 생성
재귀적 방법으로 실행했을 경우 O(2^n) 인데, O(N) 으로 실행시간 줄임