파이썬과 함께하는 자료구조의 이해 책 정리

그래프

광범위한 분야에서 활용되는 자료구조 ex) 인터넷, 도로, 운송, 전력, 등

그래프 용어

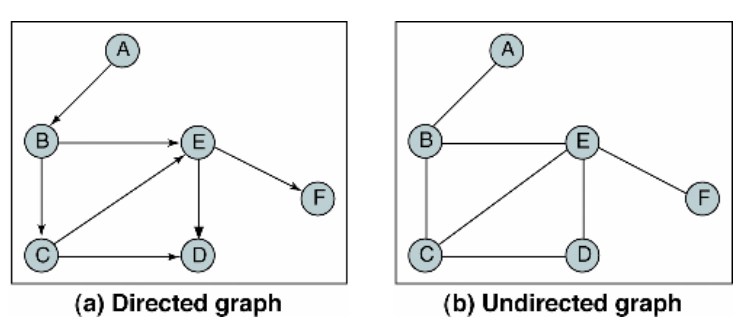
그래프는 정점(Vertex)과 간선(Edge)의 집합으로 하나의 간선은 두 개의 정점을 연결
G=(V,E) V는 정점의 집합, E는 간선의 집합
방향이 있는 그래프 방향 그래프(Directed Graph) 방향이 없는 그래프 무방향 그래프(Undirected Graph)
차수: 정점a에 인접한 정점의 수
진입차수/친출차수 : 방향그래프에서 차수를 두가지로 정의
경로 : 시작 정점부터 도착점까지의 정점들을 나열하여 표현
단순경로 : 경로 상의 정점들이 모두 다른 경로
- 즉 일반적으로 경로는 동일한 정점이 중복되어 나타날 수 있다.
사이클 : 시작 정점과 도착점이 동일한 단순 경로
연결성분 : 그래프에서 정점들이 서로 연결되어 있는 부분을 의미
가중치 그래프 : 간선에 가중치가 부여된 그래프, 가중치는 실제 두 정점 사이의 거리 혹은 두 정점을 연결하는 간선을 지나는데 소요되는 시간 / 응용에 따라 음수일 수도 있음
부분그래프 : 그래프의 정점과 간선의 일부분으로 이루어진 그래프
- 참고 자료 블로그
- 트리 : 싸이클이 없는 그래프
- 신장트리 : 주어진 그래프가 하나의 연결성분으로 구성되어있을 때, 그래프의 모든 정점들을 싸이클 없이 연결하는 부분그래프

그래프 자료구조

그래프를 자료구조로서 저장하기 위한 방법으로 인접행렬 과 인접 리스트를 주로 사용한다.
희소그래프 : 간선 수는 최대 간선 수인 N(N-1)/2 보다 작다. 실세계의 대부분의 그래프
조밀그래프 : 간선의 수가 최대 간선 수에 근접한 그래프

인접행렬

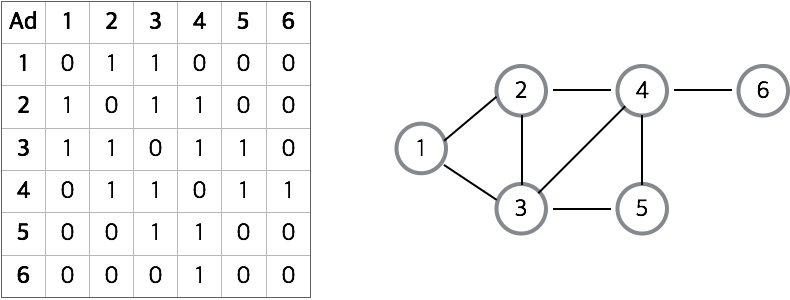
N개의 정점을 가진 그래프의 인접행렬은 2차원 리스트에 저장가능하다.
- ex) 인접행렬 저장할 리스트가 a라면 정점들을 0,1,…,N-1
- i 와 j사이에 간선이 없으면 a[i][j] = 0, 간선이 있으면 a[i][j] = 1로 표현
가중치 그패으 경우 1대신 가중치를 저장

인접 리스트

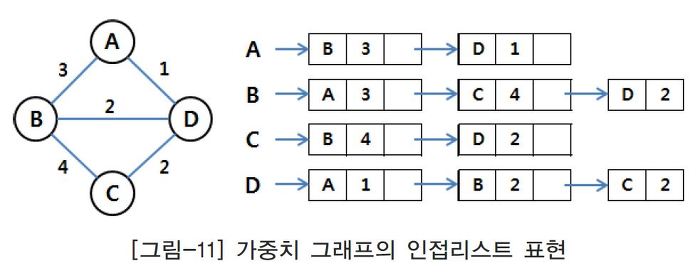
각 정점마다 1개의 단순연결리스트 사용하여 인접한 각 정점을 노드에 저장
파이썬에서는 리스트로 그래프를 표현 할 수 있다. 이 구현은 인접행렬과 인접리스트를 동시에 반영 한 것이라고 할 수 있다.

깊이우선탐색과 너비우선탐색

깊이우선탐색 / 너비우선탐색 : 신증트리, 연결성분, 경로, 사이클
최소 간선을 사용하는 경로 : BFS(너비우선)
위상정렬, 이중연결성분, 강연결성분 : DFS(깊이우선)

깊이우선탐색(Depth First Search)

임의의 정점에서 시작하여 이웃하는 하나의 정점을 방문하고, 방금 방문한 정점의 이웃 정점을 방문하여, 이웃하는 정점들을 모두 방문한 경우에 이전 정점으로 돌아가 탐색을 수행 하는 방식
미로에서 출구 찾는 것과 비슷

수행시간

DFS의 수행시간은 탐색이 각 정점을 한번씩 방문하여 각 간선을 1번씩만 사용하여 탐색하기 때문에 O(N+M)이다. N은 그래프 정점 수, M은 간선 수

코드

다른 코드 [참고 코드 블로그]((http://paper-ship.tistory.com/2)

def DFS(adj, s):
    tovisit = [s]
    visited = []
    while tovisit:
        u = tovisit.pop()
        visited.append(u)
        for v in adj[u]:
            if v not in visited + tovisit:
                tovisit.append(v)
    return visited


G1 = {1: [2, 3], 2: [3, 4, 5], 3: [5, 7, 8], 4: [5], 5: [6], 6: [], 7: [8], 8: []}
print(DFS(G1, 1))

책에 나온 코드 ```python
그래프 인접리스트

ajd_list = [ [2, 1], [3, 0], [3, 0], [9, 8, 2, 1], [5], [7, 6, 4], [7, 5], [6, 5], [3], [3] ]

N = len(ajd_list)

저점 방문 여부 확인 용

visited = [False] * N

def dfs(v): visited[v] = True print(v, ‘ ‘, end=’’) for w in ajd_list[v]: if not visited[w]: # 정점) w에 인접한 정점으로 dfs()재귀호출 dfs(w)

if name == ‘main’: print(‘DFS 방문순서’) for i in range(N): if not visited[i]: dfs(i)

- 깊이우선 신장트리 : DFS를 수행하며 실선으로 만들어지는 트리(실선 : 탐색 중 이미 정점에 도달한 경우 나타냄)

---

## 너비우선탐색(BFS:Breadth First Search)
- 임의의 정점 s에서 시작하여 s의 이웃하는 모든 정점들을 방문하고, 방문한 정점들의 이웃 정점들을 방문하는 방식으로 그래프의 모든 정점을 방문한다. 이진트르이 레벨순회와 비슷하다.
- 큐 자료구조를 사용한다.
- 교차간선 : 탐색 중 이미 방문된 정점에 도달 한 경우
- 너비우선 진장트리

### 수행시간
- BFS는 DFS 같이 각 정점을 1번씩 방문하여, 각 간선을 1번씩만 사용하여 탐색하기 때문에 `O(N+M)`의 수행시간이 소요된다. ㅏ
- 두개의 탐색 방법은 방문순서나 간선을 사용하는 순서만 다를 뿐이다.

### 코드
```python
# 그래프 인접리스트
ajd_list = [
    [2, 1], [3, 0], [3, 0], [9, 8, 2, 1],
    [5], [7, 6, 4], [7, 5], [6, 5], [3], [3]
]

N = len(ajd_list)
# 저점 방문 여부 확인 용
visited_dfs = [False] * N


def bfs(i):
    queue = []
    visited_dfs[i] = True
    queue.append(i)

    while len(queue) != 0:
        # 큐가 맨 앞에서 제거된 정점을 v가 참조하게함
        v = queue.pop(0)
        print(v, ' ', end='')
        for w in ajd_list[v]:
            if not visited_dfs[w]:
                visited_dfs[w] = True
                # v에 인접하면서 방문 안된 정점 큐에 삽입
                queue.append(w)


if __name__ == '__main__':
    print('BFS 방문순서')
    for i in range(N):
        if not visited_dfs[i]:
            bfs(i)