파이썬과 함께하는 자료구조의 이해 책 정리
트리 자료구조
- 파이썬 리스트나, 연결리스트는 데이터를 일렬로 저장하기 때문에, 탐색 연산이 순차적으로 수행된다는 단점이 있다. 파이썬 리스트는 미리 정렬해 놓으면 이진탐색 을 통해 효울적인 탐색이 가능하지만, 삽입이나 삭제 후에도 정렬 상태를 유지해야 하기 때문에 삽입 삭제하는데 O(N) 시간이 소요된다. 이러한 문제검을 보완하는 것이 트리이다.
- 트리는 기관의 계층구조, 컴퓨터 운영체제의 파일 시스템 등이 예로 있다.
- 트리는 이진트리와 트리로 구분되고 이진트리는 다양한 탐색트리, 힙, 자료구조, 컴파일러의 수식을 위한 구문트리 등이 있다.
트리(Tree)
- 트리는 비어있거나, 아니면 루트 R과 트리의 집합으로 구성되는데, 각 트리의 루트는 R의 자식노드이다. 트리는 공집합 일 수도 있다.
용어정리
- 루트(Root) : 트리 최상위에 있는 노드 ex) A
- 자식(Child) 노드 : 노드 하위에 연결된 노드 ex) B,C,D,E,F,G,H,I,J,K,L,M
- 차수(Deggree) : 자식노드 수 ex) A의 차수는 3
- 부모(Parent)노드 : 노드의 상위에 연결된 노드 ex) A,B,C,D,E,H
- 이파리(Leaf) : 자식이 없는 노드 ex)F,G,I,J,K,L,M
- 형제(Sibling)노드 : 동일한 부모를 가지는 노드 ex) B,C,D
- 조상(Ancestor)노드 : 루트까지의 경로상에 있는 모든 노드들의 집합 ex) M의 조상 노드 A,D,H
- 후손(Descendant)노드 : 노드 아래로 매달린 모든 노드들의 집합
- 서브트리(Subtree) : 노드 자신과 후손노드로 구성된 트리
- 레벨(Levle) : 루트가 레벨 1에 있고, 아래층으로 내려가며 레벨이 1씩 증가, 깊이와 같다 ex) 레벨 4
- 높이(Height) : 트리의 최대 레벨
- 키(Key) : 탐색에 사용되는 노드에 저장된 정보
- 이파리는 단말노드 혹은 외부 노드 라고도 한다.
- 이파리가 아닌 노드(자식이 있는 노드) 내부 노드 또는 비 단말노드라고도 한다.
일반적인 트리 저장 방법
- 메모리에 저장하기 위해 각 노드에 키와 자식 수만큼 레퍼런스를 저장한다.
- 최대 차수가 k인 트리에 N개의 노드가 있다면, None 레퍼런스 수는
Nk - (N-1) = N(k-1)+1이다. Nk는 총 레퍼런스 수이고, (N-1) 은 트리에서 실제 부모 자식을 연결하는 레퍼런스 수이다. 따라서 k가 클수록 메모리의 낭비가 심해지는 것은 물론, 트리 탐색하는 과정에서 None 레퍼런스를 확인해야 하므로 시간적으로도 매우 비효울적이다.
왼쪽자식-오른쪽 형제
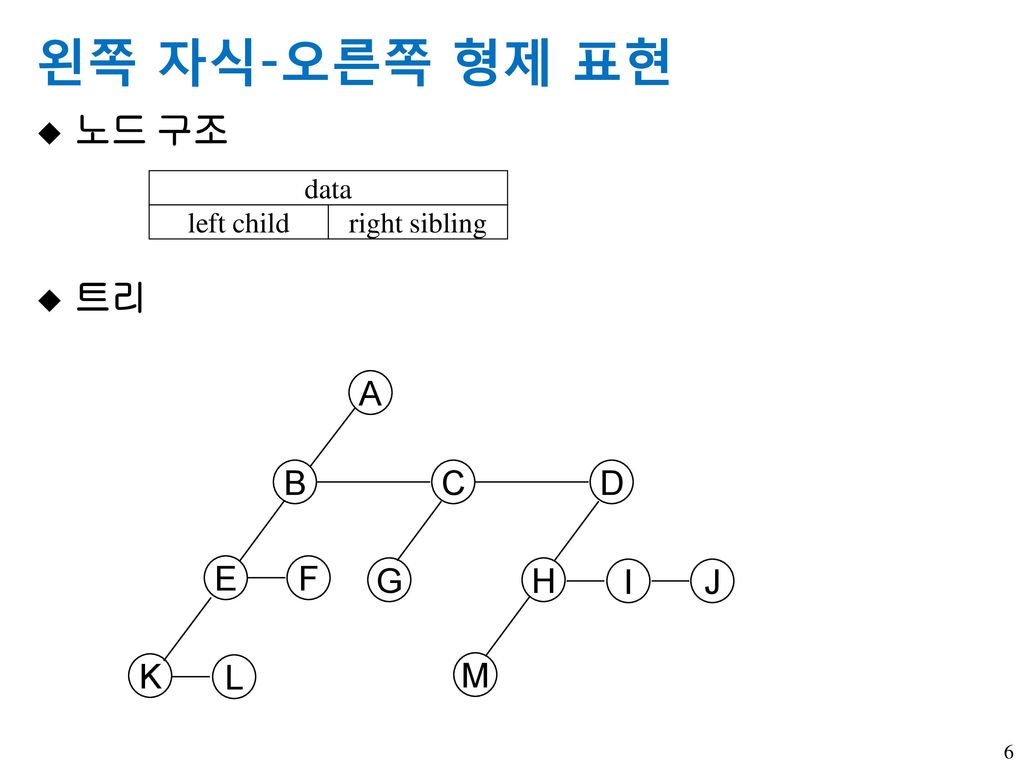
- 위와 같은 단점을 보완하기 위해 만들어진 자료구조다. 노드의 왼쪽 자식과 왼쪽자식의 오른쪽 형제노드를 가르키는 2개의 레퍼런스 만을 사용하여 노드를 표현 할 수 있다.
- 노드의 차수가 일정하지 않은 일반적인 트리를 구현하는데 효율적인 자료구조 ex)HTML,XML의 문서 트리, 운영체제의 파일시스템, 탐색트리 등에 사용됨
이진트리(Binary Tree)
- 각 노드의 자식 수가 2이하인 트리
- 컴퓨터 분야에서 가장 많이 사용되는 자료구조이다. 왜냐하면 데이터의 구조적인 관계를 잘 반영하고, 효율적인 삽입과 탐색이 가능하다. 또한 이진트리의 서브트리를 다른 이진트리의 서브트리와 교환하는 것이 쉽다.
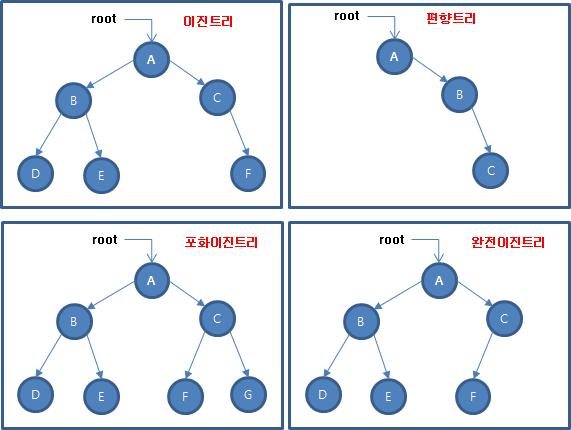
이진트리 종류
- 포화이진트리(Full Binary Tree) 는 모든 이파리의 깊이가 같고, 각 내부노드가 2개의 자식노드를 가진 트리
- 완전이진트리(COmplete Binary Tree) 는 마지막 레벨을 제와한 각 레벨이 노드들로 꽉 차있고, 마지막 레벨에는 노드들이 왼쪽부터 빠짐없이 채워진 트리
이진트리의 레벨과 노드수의 관계
- 레벨 k에 있는 최대 노드수 2k-1이다.
- 높이가 h인 포화이진트리에 있는 노드 수는 2h-1이다.
- N개의 노드를 가진 완전이진트리의 높이는 log2(N+1)
리스트를 사용하는 경우
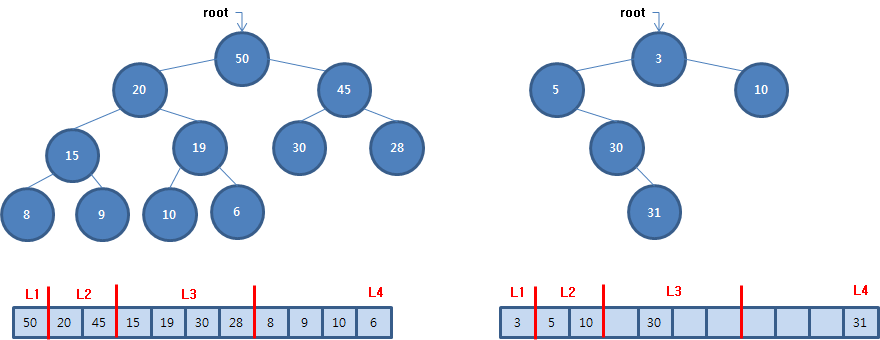
- a[i]의 부모는 a[i//2]에 있다. 단 i>1
- a[i]의 왼쪽 자식은 a[2i]에 있다.단 2i<=N이다.
- a[i]의 오른쪽자식은 a[2i+1]에 있따. 단 2i+1 <=N 이다.
- 이진트리를 리스트에 저장하면 노드의 부모노드와 자식노드가 리스트 어디에 저장되어있는지를 쉽게 알 수 있다.
- 완전이진트리의 경우 자식노드들을 참조할 레퍼런스를 저장할 메모리 공간이 필요없기 때문에 매우 효율적이다. 그러나 편향이진트리를 리스트에 저장하는 경우, 트리의 높이가 커질 수록 메모리 낭비가 심해진다.
레퍼런스를 이용한 경우
코드
class Node:
def __init__(self, item, left=None, right=None):
self.item = item
self.left = left
self.right = right
class BinaryTree:
def __init__(self):
# 트리 생성자
# 트리 루트
self.root = None
def preorder(self, n):
# 전위순회
if n is not None:
# 맨 먼저 노드 방문
print(str(n.item), '', end='')
# 왼쪽 서브트리 방문 후, 오른쪽 서브트리 방문
if n.left:
self.preorder(n.left)
if n.right:
self.preorder(n.right)
def inorder(self, n):
# 중위 순회
if n is not None:
if n.left:
self.inorder(n.left)
print(str(n.item), '', end='')
if n.right:
self.inorder(n.right)
def postorder(self, n):
# 후위 순회
if n is not None:
if n.left:
self.postorder(n.left)
if n.right:
self.postorder(n.right)
print(str(n.item), '', end='')
def levelorder(self, root):
# 레벨 순회
q = []
q.append(root)
while len(q) is not 0:
t = q.pop(0)
print(str(t.item), '', end='')
if t.left is not None:
q.append(t.left)
if t.right is not None:
q.append(t.right)
def height(self, root):
if root is None:
return 0
# max(iterable)는 인수로 반복 가능한 자료형을 입력받아 그 최대값을 리턴하는 함수이다.
return max(self.height(root.left), self.height(root.right))+1
if __name__ == '__main__':
t = BinaryTree()
n1 = Node(100)
n2 = Node(200)
n3 = Node(300)
n4 = Node(400)
n5 = Node(500)
n6 = Node(600)
n7 = Node(700)
n8 = Node(800)
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
n3.left = n6
n3.right = n7
n4.left = n8
t.root = n1
print('트리 높이=', t.height(t.root))
print('전위순회:', end='')
t.preorder(t.root)
print('\n중위순회:', end='')
t.inorder(t.root)
print('\n후위순회:', end='')
t.postorder(t.root)
print('\n레벨순회:', end='')
t.levelorder(t.root)
코드 실행
트리 높이= 4
전위순회:100 200 400 800 500 300 600 700
중위순회:800 400 200 500 100 600 300 700
후위순회:800 400 500 200 600 700 300 100
레벨순회:100 200 300 400 500 600 700 800
이진트리연산
- 트리를 순회하는 중에 노드를 방문하는 시점에 따라 구분한다. 모든 루트로부터 동일한 순서로 이진트리의 노드들을 지나가는데, 특정 노드에 도착하자마자 그 노드를 방문하는지, 혹은 지나치고 나중에 방문하는지에 따라 구분
전위순회(NLR)
- 노드 n에 도착하면 n을 먼저 방문하고 왼쪽 자식노드로 순회를 계속한다. 그 후엔 오른쪽 서브트리의 모든 후손 노드들을 방문한다.
중위순회(LNR)
- 노드 n에 도착하면 방문을 보류하고 n의 왼쪽 서브트리로 순회를 진행한다. 그리고 나서 n을 방문하고 오른쪽 서브트리를 방문
후위순회(LRN)
- 노드 n에 도착하면 왼쪽 서브트리를 순회하고 오른쪽 서브트리를 순회한뒤 마지막으로 n을 방문한다.
레벨순회
수행시간
- 각 노드를 1번씩만 방문하므로 O(N) 시간이 소요된다.
이진트리 그외 방법
- 이진트리의 기본 연산은 레벨순회를 제외하고 모두 스택 자료구조를 사용한다. (함수의 재귀호출 시스템 스택을 사용하므로) 따라서 스택에 사용되는 메모리 공간의 크니는 트리의 높이에 비례한다.
- 스택없이 이진트리 연산을 하는 방법은
Node에 부모노드를 가리키는 레퍼런스 필드를 추가로 선언하여 순횐하는 방법과 스테드 이진트리라는 방법이 있다. 이는노드의 None레퍼런스 활용 = None레퍼런스 공간에 다음 방문할 노드의 레퍼런스를 저장하는 것을 말한다.
스레드 이진트리
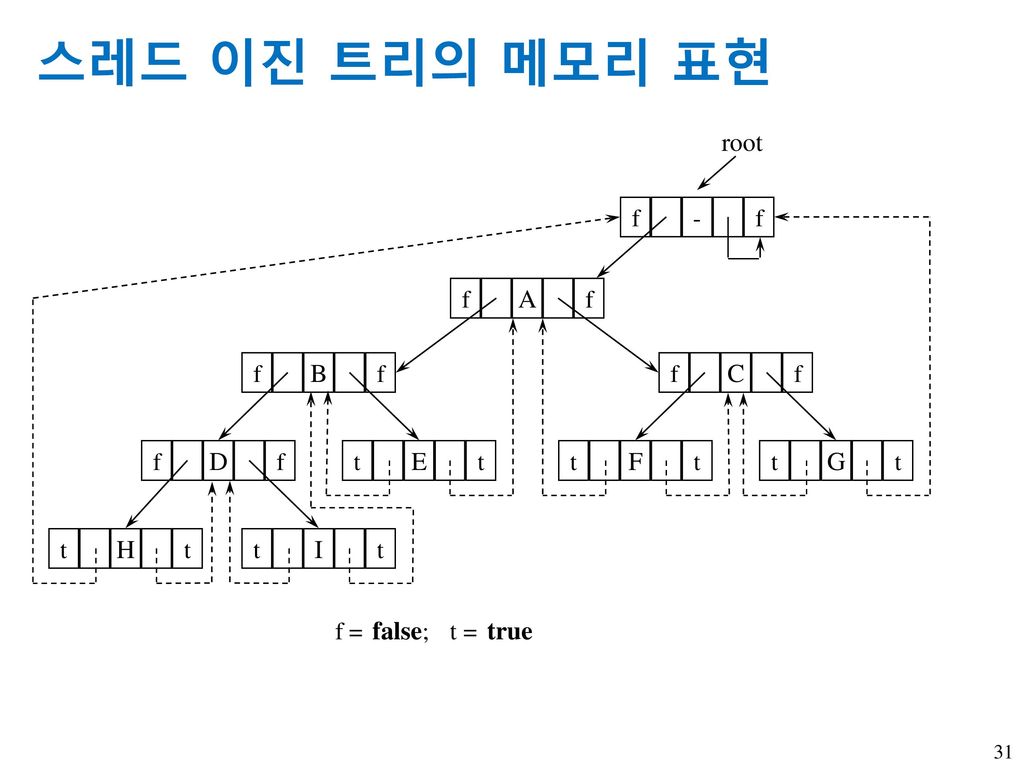
- 각 노드의 오른쪽 None 레퍼런스는 다음 방문할 노드를 참조하고, 각 노드의 왼쪽 None 레퍼런스는 직전 방문한 노드를 참조하게 한 이진트리
- 이전에 방문한 노드와 앞으로 방문할 노드를 가리키도록 만들어서 순회 연산 스택이 없어도 수행될 수 있도록 만든 것
- N+1개의 None레퍼런스 필드
- 각 노드마다 2개의 레퍼런스 필드(left, right)가 있으므로 총 2N개의 레퍼런스 필드가 존재
- 부모자식을 연결하는 레퍼런스는 N-1 : 루트를 제와한 각 노드가 1개의 부모 노드를 갖기 때문
- 대부분 중위순회에 기반하여 구현되나, 후외나 전위도 구현가능하다.
- 스택을 사용한 순회보다 빠르게 메모리 공간도 적게 차지한다는 장점이 있다.
- 그러나 잦은 데이터 삽입과 삭제는 구현이 비교적 봅작한 편이므로 좋은 성능을 보여주지 못한다.
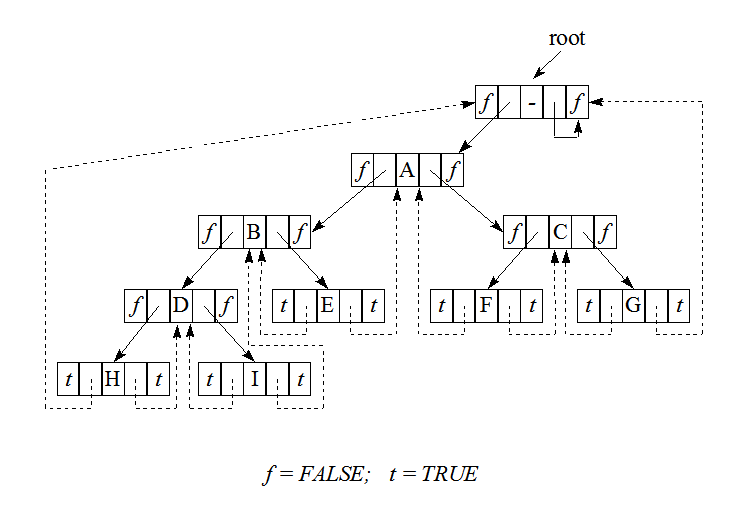
- Node 객체에 2개의 Boolean필드를 사용하여 레퍼런스가 스레드(다음 방문할 노드)로 사용되는 것인지 아니면 left 나 right 트리의 부모, 자식 사이의 레퍼런스인지 True, False 로 표시해야한다.
- 참고 사이트 boolean필드 관련
- 참고 사이트 노드 계산 관련