이진힙(Binary Heap)

파이썬과 함께하는 자료구조의 이해 책 정리

우선순위큐

가장 높은 우선순위를 가진 항목에 접근하거나 해당 항목을 삭제하는 연삼과 임의의 우선순위를 가진 항목을 삽입하는 연산을 지원하는 자료구조
스택이나 큐도 일종의 우선순위 큐이다.
- 스택의 경우 가장 마지막으로 삽입된 항목이 가장 높은 우선순위를 가진다.최근 시간일수록 높은 우선순위가 부여된다.
- 큐는 먼저 삽입된 항목이 우선순위가 더 높고 이른 시간일 수록 더 높은 우선순위를 부여한다.

왜 또다른 우선순위큐 자료구조가 필요할까?

스택에 새로 삽입되는 항목의 우선순위는 스택에 저장된 모든 항목들의 우선순위보다 높고, 큐에 새롭게 삽입되는 항목의 우선순위는 큐에 저장되어 있는 모든 항목들보다 우선순위가 낮다. 새롭게 삽입되는 항목이 임의의 우선순위를 가진다면 스택이나 큐는 새 항목이 삽입될때마다 항목들을 우선순위에 따라 정렬된 상태를 유지 해야 한다는 문제점이 있다.
새 항목 삽입 시 정렬된 상태를 유지할 필요 없고, O(1) 시간에 가장 높은 우선순위를 가진 항목에 접근 가능하며, 가장 높은 우선순위를 가진 항목을 삭제하는 연산을 지원하는 것이 이진힙 이다.

이진힙

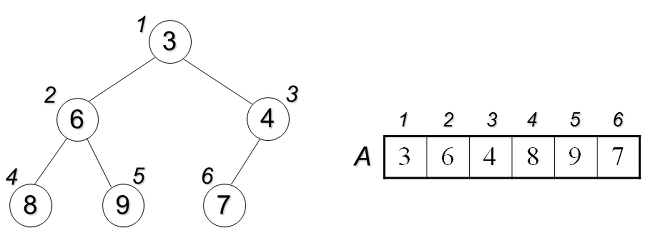
a[i]은 자식은 a[2i]와 a[2i+1]에 있다.
a[j]의 부모는 a[2//j]에 있다. 단 j > 1 이다.

우선순위큐를 구현하는 가장 기본적인 구조.
완전이진트리로서 부모의 우선순위가 자식의 우선순위보다 높은 자료구조
힙속성 : 부모의 우선순위가 자식의 우선순위보다 높은 것
완전이진트리는 1차원 리스트로 구현하며, 리스트의 두번째 원소부터 사용한다. 즉 a[1]부터 차례로 저장한다.

최소힙

키가 작을수록 높은 우선순위를 가진다
최소힙의 루트에는 항상 가장 작은 키가 저장된다. 최소힙의 노드에 저장된 키값이 자식 노드의 키값보다 작다는 규칙
O(1) 시간에 가장 작은 키를 가진 노드에 접근할 수 있다.

최솟값 삭제

루트의 키를 삭제
힙의 마지막 노드, 즉 리스트의 가장 마지막 항목을 루트로 옮기고 힙 크기 1 감소
다음으로 루트로부터 자식들 중에서 작은 값을 가진 자식과 키를 비교하여 힙속성이 만족될 때까지 키를 교환하며 이파리 방향으로 진행
downheap 루트로부터 아래로 내려가며 진행되는 것

삭제 연산

힙의 마지막 노드(데이터를 가진 리스트의 마지막 항목)의 뒤에 새로운 항목을 추가시킨 후, 루트방향으로 올라가면서 부모노드의 키와 비교하여 힙속성이 만족될 때까지 노드 교환
upheap 이파리노드로부터 위로 올라가며 진행되는 것

최대힙

키가 클수록 높은 우선순위를 가진다.

수행시간

힙에서 각 연산의 수행시간은 힙의 높이에 비례한다. 힙은 완전이진트리이므로 힙에 N개의 노드가 있으면 그 높이는 [log_(N+1)] 이다.
수행시간은 O(log_N) 이다.

코드

class BHeap:
    def __init__(self, a):
        # 리스트 a
        self.a = a
        # 항목 수 N
        self.N = len(a) - 1

    def create_heap(self):
        # 초기 힙 만들기 = 상향식 힙 만들기
        # 초기에 임의의 순서로 키가 저장되어 있는 리스트 a[1]~a[N]의 항목들을 최소힙으로 만든다.
        # a[1]을 downheap하여 최소힙을 만드는 것을 의미
        # a[N//2+1] ~ a[N] 에 대하여 downheap 을 수행하지 않는 이유는 이 노드들이 이파리이므로
        # 각각의 노드가 힙 크기가 1인 독립적인 최소힙이기 때문이다.
        for i in range(self.N // 2, 0, -1):
            self.downheap(i)

    def insert(self, key_value):
        self.N += 1
        self.a.append(key_value)
        self.upheap(self.N)

    def delete_min(self):

        if self.N == 0:
            print('힙이 비어있음')
            return None

        minimum = self.a[1]
        self.a[1], self.a[-1] = self.a[-1], self.a[1]
        del self.a[-1]
        self.N -= 1
        self.downheap(1)
        return minimum

    def downheap(self, i):

        while 2 * i <= self.N:
            # 왼쪽, 오른쪽 자식중에서 승자 결정
            k = 2 * i

            if k < self.N and self.a[k][0] > self.a[k + 1][0]:
                k += 1
            # 힙속성 만족하면, 루프 나가기
            if self.a[i][0] < self.a[k][0]:
                break
            # 자식 승자와 현재 노드 교환
            self.a[i], self.a[k] = self.a[k], self.a[i]
            i = k

    def upheap(self, j):
        while j > 1 and self.a[j // 2][0] > self.a[j][0]:
            # 부모와 자식 교환
            self.a[j], self.a[j // 2] = self.a[j // 2], self.a[j]
            # 현재 노드가 한단계 위로 올라감
            j = j // 2

    def print_heap(self):
        for i in range(1, self.N+1):
            print(f'[{self.a[i][0]}, {self.a[i][1]}]', end='')
        print('\n 힙 크기 = ', self.N)


if __name__ == '__main__':
    a = [None] * 1
    a.append([90, 'watermelon'])
    a.append([80, 'pear'])
    a.append([70, 'melon'])
    a.append([50, 'lime'])
    a.append([60, 'mango'])
    a.append([20, 'cherry'])
    # a.append([30, 'grape'])
    # a.append([35, 'orange'])
    # a.append([10, 'apricot'])
    # a.append([15,'banana'])
    # a.append([45,'lemon'])
    # a.append([40,'kiwi'])
    # print(a)
    b = BHeap(a)
    b.print_heap()

    b.create_heap()
    print("최소힙")
    b.print_heap()

    print('최솟값 삭제 후')
    print(b.delete_min())
    b.print_heap()

    b.insert([5,'apple'])
    print('5 삽입 후')
    b.print_heap()

코드 실행

[90, watermelon][80, pear][70, melon][50, lime][60, mango][20, cherry]
 힙 크기 =  6
최소힙
[20, cherry][50, lime][70, melon][80, pear][60, mango][90, watermelon]
 힙 크기 =  6
최솟값 삭제 후
[20, 'cherry']
[50, lime][60, mango][70, melon][80, pear][90, watermelon]
 힙 크기 =  5
5 삽입 후
[5, apple][60, mango][50, lime][80, pear][90, watermelon][70, melon]
 힙 크기 =  6